本文共 2662 字,大约阅读时间需要 8 分钟。
近年来,区块链在解决信任问题上具有先天优势,许多上市企业以及传统机构纷纷在其领域展开探索和研究。区块链最具价值的优势是将平等且有竞争关系的各参与方链接在一起,但在实践的过程中却发现,由于涉及到数据存储、密码学、共识机制等多种计算机技术,对专业性要求极高,加上目前的区块链项目大多缺乏清晰的运营及盈利模式,其具体价值也难以估值。
企业之间难以平衡数据隐私和数据共享的矛盾、区块链的计算能力和交易性能不足等都给创新的区块链在金融方向的应用提出了挑战。区块链想要大规模的落地,就必须和外部数据进行关联,并将真正具有实用性的产品融入到现实世界对应的场景中。但区块链本身是一个封闭的确定性的系统,只能获取到链内的数据,而不能主动调取或访问到链外真实世界的数据。
早前,在中国人民银行发布的《区块链能做什么?不能做什么?》的报告中,是这样对预言机定义的:“区块链外信息写入区块链内的机制,一般被称为预言机(Oracle mechanism)”。
预言机能够更快地获取链上数据,它允许确定的智能合约对不确定的外部世界作出反应,是智能合约与外部进行数据交互的唯一途径。预言机的出现给当下市场提供了一个很好的解决办法,不仅允许将与真实事件有关的数据调用到区块链上,包括基于现有资产价格的自动化交易以及各类游戏dApp的实时金额支付,还会为智能合约提供触发和执行规则所需的数据,将发生在链上的事件通知链外的参与者。
DeFi结合
事实上,DeFi为了保持去中心化的状态,使用的数据不能由中心化的来源提供,因为当中可能会涉及伪造、篡改、修改或隐藏信息。DeFi协议将预言机作为区块链之外的数据来源,例如资产市场价格、体育赛事结果、天气数据或任何其他在区块链上无法获得的信息,如果没有预言机,DeFi协议就无法获得正常运行所需的所有数据。

金融衍生品是目前全世界价值最大的市场,市值大约500万亿到1200万亿美元之间。因为几乎所有拥有价值的事物都能够被作为金融衍生品标的物,而基于这些标的物可以建立许多不同种类的金融衍生品,如此庞大的体系加上四通八达的环境,交易过程实际涉及巨大风险。预言机可以更好地维护、执行和交割衍生品合约,资金可以托管在智能合约中,衍生品合约自动执行,状态改变数据也一一被记录在案,加上智能合约可获取关于标的资产的市场数据,并连接至合约交割所需的外部系统,如支付、监管合规及审计等系统,可以防范重大疏漏导致全球金融的系统性风险。
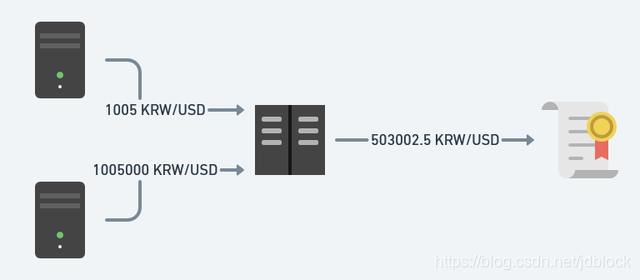
知名的衍生品交易平台 Synthetix 在 19 年 6 月份遭遇了攻击,损失超过 3700 万枚 sETH,原因是Synthetix所依赖的其中一个价格推送错误地报告了韩元的价格,比真实汇率高出1000倍,由于价格预言机系统的其他地方出现了其他的错误,这个价格被系统接受并发布在链上,在链上一个交易机器人迅速在sKRW市场上进行了买入和卖出。归其深入,DeFi当中的大多数项目仍然趋向于选择使用自己搭建的预言机服务,这极易造成单点故障、易受攻击等问题,复杂且场景丰富的DeFi世界需要更全面的预言机产品来实现应用落地。
预言机市场正变得有趣和多元
不少学者及研究人士通过调查后发现,更多的DeFi用户和开发者愿意为可靠和防篡改的数据付费,这无疑让区块链领域的盈利模式变得更为清晰。越来越多的项目开始着手于提高预言机提供数据的准确性和去中心化水平所需要的解决方案,即使是像币安这样的老牌交易所,也在其新推出的公链上积极拓展预言机的项目合作,以此来为DeFi协议提供数字货币价格数据,这进一步证明这是一个有利可图的市场,事情也变得更加有趣起来。

Paralink Network是基于波卡生态的跨链应用程序的真实数据入口,实现跨链互操作性和可扩展性的前提下,低交易成本和更高的吞吐量使其成为Oracle解决方案提供实时和成本可访问的数据的新兴预言机范例,并更具安全性,截止目前为止,Paralink Network系统遭遇黑客攻击为零。据了解,Paralink Network的优质技术目前已经被广泛应用于衍生品和加密货币市场的事实资产喂价、预测市场和保险的决议层以及区块链游戏的硬件服务。
4月28日,Paralink Network与OpenDeFi建立战略合作关系,旨在为全球用户提供各种DeFi解决方案。OpenDeFi联合创始人塔鲁沙·米塔尔(Tarusha Mittal)表示:“我们很高兴有机会与Paralink合作,OroPocket的OpenDeFi通过消除传统银行系统随附的费时乏味的代码,开创了资产支持银行系统的先驱,”“我们赞扬Paralink与我们一起开发巨大的DeFi市场机会。”并希望通过这次合作,OpenDeFi将利用Paralink的多链预言机,为网络上的成员和应用程序获取可靠的数据提要和定价。5月,Paralink Network正式成为Genpad生态合作伙伴,帮助平台获得安全可靠的价格信息,释放去中心化金融潜力。

结论
预言机在关于大规模应用、速度、安全性、去中心化等问题上有待发展,不可否认的是它正在经历项目发展阶段必经的磨合期。作为DeFi 安全性的一个重要组成部分,无论是价格还是支付的数据,预言机蕴藏的巨大能量仍然是不可忽视的关键工具。目前而言,市面上预言机主要的应用场景有保险、溯源等,未来可用于IOT领域以及传统金融板块,帮助实现需要与外部世界交互的应用场景,加速区块链发展和应用落地。
转载地址:http://hfqiz.baihongyu.com/